CSC300: Union Find

Contents [0/10]

Video [1/10]

Notes from the textbook [2/10]

TestUF [3/10]

QuickFind [4/10]

QuickUnion [5/10]

Weighted [6/10]

Compression [7/10]

Weighted Compression [8/10]

Weighted Compression Halving [9/10]

Comparing UF implementations [10/10]

(Click here for one slide per page)

Video [1/10]

In several parts

Open Playlist

Notes from the textbook [2/10]

In these videos I will use some notes from the textbook:

TestUF [3/10]

file:TestUF.java [source] [doc-public] [doc-private]

package algs15;
import java.util.Scanner;
import stdlib.*;

public class TestUF {
  public static enum Order { ZERO_I, I_ZERO, I_MINUS, MINUS_I, RANDOM }
  public static void main(String[] args) {
    show(10, "4 3, 3 8, 6 5, 9 4, 2 1, 8 9, 5 0, 7 2, 6 1, 1 0, 6 7"); //textbook tinyUF.txt    
    show(10, "0 1, 0 2, 0 3, 0 4, 0 5, 0 6, 0 7, 0 8, 0 9"); // ZERO_I
    show(10, "1 0, 2 0, 3 0, 4 0, 5 0, 6 0, 7 0, 8 0, 9 0"); // I_ZERO
    show(10, "1 0, 2 1, 3 2, 4 3, 5 4, 6 5, 7 6, 8 7, 9 8"); // I_MINUS
    show(10, "0 1, 1 2, 2 3, 3 4, 4 5, 5 6, 6 7, 7 8, 8 9"); // MINUS_I
    show(16, "0 1, 2 3, 4 5, 6 7, 8 9, 10 11, 12 13, 14 15," + "0 2, 4 6, 8 10, 12 14," + "0 4, 8 12," + "0 8");
    showRandom(12);
    double prevUnion = 0;
    double prevConnected = 0;
    for (int N = 128; N<=MAX; N += N) {
      timeTrial(N, Order.RANDOM);
      StdOut.format("N=%,13d Union=%7.3f [%8.3f] Connected=%7.3f [%8.3f]\n", N, timeUnion, timeUnion/prevUnion, timeConnected, timeConnected/prevConnected);
      prevUnion = timeUnion;
      prevConnected = timeConnected;
    }
  }
  private static int MAX=50_000_000;
  private static UF getUF (int N) {
      MAX=500_000; return new QuickFindUF(N);  //   (262_144,RANDOM) Union ~ 36  Connected ~ .006
      //MAX=500_000; return new QuickUnionUF(N); //   (262_144,RANDOM) Union ~ 17  Connected ~ 18
    //return new WeightedUF(N);                //(33_554_432,RANDOM) Union ~ 10  Connected ~ 10
    //return new CompressionUF(N);             //(33_554_432,RANDOM) Union ~ 16  Connected ~ 7
    //return new XWeightedHalvingUF(N);        //(33_554_432,RANDOM) Union ~  9  Connected ~ 6
    //return new XWeightedCompressionUF(N);    //(33_554_432,RANDOM) Union ~  9  Connected ~ 6
  }
  
  private static double timeUnion;
  private static double timeConnected;
  private static void timeTrial(int N, Order order) {
    UF ufTime = getUF(N);       
    SHOW_COMPRESSION_STEPS = false;
    Stopwatch sw1 = new Stopwatch();
    for (int i=1; i<N; i+= 1) {
      int p = StdRandom.uniform(N);
      int q = StdRandom.uniform(N);
      switch (order) {
      case ZERO_I: ufTime.union (0, i); break; 
      case I_ZERO: ufTime.union (i, 0); break; 
      case I_MINUS: ufTime.union (i, i-1); break;
      case MINUS_I: ufTime.union (i-1, i); break;
      case RANDOM: ufTime.union (p, q); break;
      }
    }
    timeUnion = sw1.elapsedTime();

    Stopwatch sw2 = new Stopwatch();    
    for (int i=1; i<N; i+= 1) {
      int p = StdRandom.uniform(N);
      int q = StdRandom.uniform(N);
      ufTime.connected(p, q);
    } 
    timeConnected = sw2.elapsedTime();
  }
  
  public static boolean SHOW_COMPRESSION_STEPS=false;
  private static void showRandom (int N) {
    SHOW_COMPRESSION_STEPS = true;
    UF uf = getUF(N);
    uf.toGraphviz();
    StdOut.format("       %2d%s\n", uf.count(), uf);
    for (int i=1; i<4*N; i++) {
      int p = StdRandom.uniform(N);
      int q = StdRandom.uniform(N);
      if (uf.connected(p, q)) {
        StdOut.format("%2d %2d: connected\n", p, q); 
      } else {
        uf.union(p, q);
        uf.toGraphviz();
        StdOut.format("%2d %2d: %2d%s\n", p, q, uf.count(), uf);
      }
    }
    StdOut.println();
  }
  private static void show (int N, String input) {
    SHOW_COMPRESSION_STEPS = true;
    Scanner s = new Scanner(input);
    s.useDelimiter("[\\s,]\\s*"); // use comma or space as delimiter

    UF uf = getUF(N);
    uf.toGraphviz();
    StdOut.format("       %2d%s\n", uf.count(), uf);
    while (s.hasNext()) {
      int p = s.nextInt();
      int q = s.nextInt();
      if (uf.connected(p, q)) {
        StdOut.format("%2d %2d: connected\n", p, q); 
      } else {
        uf.union(p, q);
        uf.toGraphviz();
        StdOut.format("%2d %2d: %2d%s\n", p, q, uf.count(), uf);
      }
    }
    StdOut.println();
    s.close();
  }
}

QuickFind [4/10]

  public int find(int p) {








    return id[p];
  }

  public void union(int p, int q) {
    int pid = find(p); // loser
    int qid = find(q); // champion
    if (pid == qid) return;
    for (int i = 0; i < id.length; i++)
      if (id[i] == pid) id[i] = qid;
    count--;
  }

Output

       10[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
 4  3:  9[0, 1, 2, 3, 3, 5, 6, 7, 8, 9]
 3  8:  8[0, 1, 2, 8, 8, 5, 6, 7, 8, 9]
 6  5:  7[0, 1, 2, 8, 8, 5, 5, 7, 8, 9]
 9  4:  6[0, 1, 2, 8, 8, 5, 5, 7, 8, 8]
 2  1:  5[0, 1, 1, 8, 8, 5, 5, 7, 8, 8]
 8  9: connected
 5  0:  4[0, 1, 1, 8, 8, 0, 0, 7, 8, 8]
 7  2:  3[0, 1, 1, 8, 8, 0, 0, 1, 8, 8]
 6  1:  2[1, 1, 1, 8, 8, 1, 1, 1, 8, 8]
 1  0: connected
 6  7: connected

N=          128 Union=  0.002 [Infinity] Connected=  0.000 [     NaN]
N=          256 Union=  0.001 [   0.500] Connected=  0.001 [Infinity]
N=          512 Union=  0.005 [   5.000] Connected=  0.000 [   0.000]
N=        1,024 Union=  0.004 [   0.800] Connected=  0.001 [Infinity]
N=        2,048 Union=  0.008 [   2.000] Connected=  0.000 [   0.000]
N=        4,096 Union=  0.010 [   1.250] Connected=  0.000 [     NaN]
N=        8,192 Union=  0.047 [   4.700] Connected=  0.000 [     NaN]
N=       16,384 Union=  0.163 [   3.468] Connected=  0.001 [Infinity]
N=       32,768 Union=  0.667 [   4.092] Connected=  0.001 [   1.000]
N=       65,536 Union=  2.857 [   4.283] Connected=  0.002 [   2.000]
N=      131,072 Union= 11.939 [   4.179] Connected=  0.002 [   1.000]
N=      262,144 Union= 46.604 [   3.904] Connected=  0.005 [   2.500]

Union is linear, Connected is constant

QuickUnion [5/10]

  public int find(int p) {
    int root = p;
    while (root != id[root])
      root = id[root];





    return root;
  }

  public void union(int p, int q) {
    int pid = find(p); // loser
    int qid = find(q); // champion
    if (pid == qid) return;
    id[pid] = qid;

    count--;
  }

Output

       10[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
 4  3:  9[0, 1, 2, 3, 3, 5, 6, 7, 8, 9]
 3  8:  8[0, 1, 2, 8, 3, 5, 6, 7, 8, 9]
 6  5:  7[0, 1, 2, 8, 3, 5, 5, 7, 8, 9]
 9  4:  6[0, 1, 2, 8, 3, 5, 5, 7, 8, 8]
 2  1:  5[0, 1, 1, 8, 3, 5, 5, 7, 8, 8]
 8  9: connected
 5  0:  4[0, 1, 1, 8, 3, 0, 5, 7, 8, 8]
 7  2:  3[0, 1, 1, 8, 3, 0, 5, 1, 8, 8]
 6  1:  2[1, 1, 1, 8, 3, 0, 5, 1, 8, 8]
 1  0: connected
 6  7: connected

N=          128 Union=  0.001 [Infinity] Connected=  0.000 [     NaN]
N=          256 Union=  0.000 [   0.000] Connected=  0.000 [     NaN]
N=          512 Union=  0.000 [     NaN] Connected=  0.000 [     NaN]
N=        1,024 Union=  0.000 [     NaN] Connected=  0.001 [Infinity]
N=        2,048 Union=  0.001 [Infinity] Connected=  0.002 [   2.000]
N=        4,096 Union=  0.001 [   1.000] Connected=  0.003 [   1.500]
N=        8,192 Union=  0.004 [   4.000] Connected=  0.014 [   4.667]
N=       16,384 Union=  0.023 [   5.750] Connected=  0.108 [   7.714]
N=       32,768 Union=  0.120 [   5.217] Connected=  0.610 [   5.648]
N=       65,536 Union=  0.529 [   4.408] Connected=  2.552 [   4.184]
N=      131,072 Union=  3.390 [   6.408] Connected= 18.097 [   7.091]
N=      262,144 Union= 17.161 [   5.062] Connected= 90.506 [   5.001]

Union is linear, Connected is linear

Weighted [6/10]

  public int find(int p) {
    int root = p;
    while (root != id[root])
      root = id[root];





    return root;
  }

  public void union(int p, int q) {
    int pid = find(p); // champion, unless q is bigger
    int qid = find(q); // loser, unless p is smaller
    if (pid == qid) return;
    if (sz[qid] > sz[pid]) { id[pid] = qid; sz[qid] += sz[pid]; }
    else                   { id[qid] = pid; sz[pid] += sz[qid]; }
    count--;
  }

Output

       10[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
 4  3:  9[0, 1, 2, 4, 4, 5, 6, 7, 8, 9]
 3  8:  8[0, 1, 2, 4, 4, 5, 6, 7, 4, 9]
 6  5:  7[0, 1, 2, 4, 4, 6, 6, 7, 4, 9]
 9  4:  6[0, 1, 2, 4, 4, 6, 6, 7, 4, 4]
 2  1:  5[0, 2, 2, 4, 4, 6, 6, 7, 4, 4]
 8  9: connected
 5  0:  4[6, 2, 2, 4, 4, 6, 6, 7, 4, 4]
 7  2:  3[6, 2, 2, 4, 4, 6, 6, 2, 4, 4]
 6  1:  2[6, 2, 6, 4, 4, 6, 6, 2, 4, 4]
 1  0: connected
 6  7: connected

N=          128 Union=  0.001 [Infinity] Connected=  0.000 [     NaN]
N=          256 Union=  0.000 [   0.000] Connected=  0.000 [     NaN]
N=          512 Union=  0.000 [     NaN] Connected=  0.000 [     NaN]
N=        1,024 Union=  0.000 [     NaN] Connected=  0.000 [     NaN]
N=        2,048 Union=  0.000 [     NaN] Connected=  0.001 [Infinity]
N=        4,096 Union=  0.001 [Infinity] Connected=  0.000 [   0.000]
N=        8,192 Union=  0.001 [   1.000] Connected=  0.001 [Infinity]
N=       16,384 Union=  0.002 [   2.000] Connected=  0.002 [   2.000]
N=       32,768 Union=  0.003 [   1.500] Connected=  0.002 [   1.000]
N=       65,536 Union=  0.004 [   1.333] Connected=  0.003 [   1.500]
N=      131,072 Union=  0.008 [   2.000] Connected=  0.008 [   2.667]
N=      262,144 Union=  0.022 [   2.750] Connected=  0.016 [   2.000]
N=      524,288 Union=  0.052 [   2.364] Connected=  0.043 [   2.687]
N=    1,048,576 Union=  0.189 [   3.635] Connected=  0.127 [   2.953]
N=    2,097,152 Union=  0.499 [   2.640] Connected=  0.427 [   3.362]
N=    4,194,304 Union=  0.841 [   1.685] Connected=  0.743 [   1.740]
N=    8,388,608 Union=  2.091 [   2.486] Connected=  1.724 [   2.320]
N=   16,777,216 Union=  4.793 [   2.292] Connected=  4.576 [   2.654]
N=   33,554,432 Union=  9.952 [   2.076] Connected=  9.855 [   2.154]

Both operations logarithmic

Compression [7/10]

  public int find(int p) {
    int root = p;
    while (root != id[root])
      root = id[root];
    while (id[p] != root) {
      int newp = id[p];
      id[p] = root;
      p = newp;
    }
    return root;
  }

  public void union(int p, int q) {
    int pid = find(p); // loser
    int qid = find(q); // champion
    if (pid == qid) return;
    id[pid] = qid;

    count--;
  }

Output

       10[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
 4  3:  9[0, 1, 2, 3, 3, 5, 6, 7, 8, 9]
 3  8:  8[0, 1, 2, 8, 3, 5, 6, 7, 8, 9]
 6  5:  7[0, 1, 2, 8, 3, 5, 5, 7, 8, 9]
 4  8>  7[0, 1, 2, 8, 8, 5, 5, 7, 8, 9]
 9  4:  6[0, 1, 2, 8, 8, 5, 5, 7, 8, 8]
 2  1:  5[0, 1, 1, 8, 8, 5, 5, 7, 8, 8]
 8  9: connected
 5  0:  4[0, 1, 1, 8, 8, 0, 5, 7, 8, 8]
 7  2:  3[0, 1, 1, 8, 8, 0, 5, 1, 8, 8]
 6  0>  3[0, 1, 1, 8, 8, 0, 0, 1, 8, 8]
 6  1:  2[1, 1, 1, 8, 8, 0, 0, 1, 8, 8]
 1  0: connected
 6  1>  2[1, 1, 1, 8, 8, 0, 1, 1, 8, 8]
 6  7: connected

N=          128 Union=  0.001 [Infinity] Connected=  0.000 [     NaN]
N=          256 Union=  0.001 [   1.000] Connected=  0.000 [     NaN]
N=          512 Union=  0.000 [   0.000] Connected=  0.000 [     NaN]
N=        1,024 Union=  0.000 [     NaN] Connected=  0.001 [Infinity]
N=        2,048 Union=  0.000 [     NaN] Connected=  0.000 [   0.000]
N=        4,096 Union=  0.000 [     NaN] Connected=  0.001 [Infinity]
N=        8,192 Union=  0.002 [Infinity] Connected=  0.001 [   1.000]
N=       16,384 Union=  0.003 [   1.500] Connected=  0.001 [   1.000]
N=       32,768 Union=  0.004 [   1.333] Connected=  0.001 [   1.000]
N=       65,536 Union=  0.004 [   1.000] Connected=  0.003 [   3.000]
N=      131,072 Union=  0.011 [   2.750] Connected=  0.005 [   1.667]
N=      262,144 Union=  0.026 [   2.364] Connected=  0.011 [   2.200]
N=      524,288 Union=  0.040 [   1.538] Connected=  0.021 [   1.909]
N=    1,048,576 Union=  0.136 [   3.400] Connected=  0.084 [   4.000]
N=    2,097,152 Union=  0.487 [   3.581] Connected=  0.285 [   3.393]
N=    4,194,304 Union=  1.331 [   2.733] Connected=  0.534 [   1.874]
N=    8,388,608 Union=  2.383 [   1.790] Connected=  1.201 [   2.249]
N=   16,777,216 Union=  6.689 [   2.807] Connected=  2.797 [   2.329]
N=   33,554,432 Union= 16.546 [   2.474] Connected=  7.270 [   2.599]

Both operations logarithmic

Weighted Compression [8/10]

  public int find(int p) {
    int root = p;
    while (root != id[root])
      root = id[root];
    while (id[p] != root) {
      int newp = id[p];
      id[p] = root;
      p = newp;
    }
    return root;
  }

  public void union(int p, int q) {
    int pid = find(p); // loser
    int qid = find(q); // champion
    if (pid == qid) return;
    if (sz[qid] > sz[pid]) { id[pid] = qid; sz[qid] += sz[pid]; }
    else                   { id[qid] = pid; sz[pid] += sz[qid]; }
    count--;
  }

Output

       10[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
 4  3:  9[0, 1, 2, 4, 4, 5, 6, 7, 8, 9]
 3  8:  8[0, 1, 2, 4, 4, 5, 6, 7, 4, 9]
 6  5:  7[0, 1, 2, 4, 4, 6, 6, 7, 4, 9]
 9  4:  6[0, 1, 2, 4, 4, 6, 6, 7, 4, 4]
 2  1:  5[0, 2, 2, 4, 4, 6, 6, 7, 4, 4]
 8  9: connected
 5  0:  4[6, 2, 2, 4, 4, 6, 6, 7, 4, 4]
 7  2:  3[6, 2, 2, 4, 4, 6, 6, 2, 4, 4]
 6  1:  2[6, 2, 6, 4, 4, 6, 6, 2, 4, 4]
 1  6>  2[6, 6, 6, 4, 4, 6, 6, 2, 4, 4]
 1  0: connected
 7  6>  2[6, 6, 6, 4, 4, 6, 6, 6, 4, 4]
 6  7: connected

N=          128 Union=  0.001 [Infinity] Connected=  0.000 [     NaN]
N=          256 Union=  0.001 [   1.000] Connected=  0.000 [     NaN]
N=          512 Union=  0.000 [   0.000] Connected=  0.000 [     NaN]
N=        1,024 Union=  0.000 [     NaN] Connected=  0.001 [Infinity]
N=        2,048 Union=  0.000 [     NaN] Connected=  0.000 [   0.000]
N=        4,096 Union=  0.000 [     NaN] Connected=  0.001 [Infinity]
N=        8,192 Union=  0.001 [Infinity] Connected=  0.001 [   1.000]
N=       16,384 Union=  0.003 [   3.000] Connected=  0.002 [   2.000]
N=       32,768 Union=  0.004 [   1.333] Connected=  0.002 [   1.000]
N=       65,536 Union=  0.003 [   0.750] Connected=  0.003 [   1.500]
N=      131,072 Union=  0.009 [   3.000] Connected=  0.007 [   2.333]
N=      262,144 Union=  0.018 [   2.000] Connected=  0.010 [   1.429]
N=      524,288 Union=  0.055 [   3.056] Connected=  0.026 [   2.600]
N=    1,048,576 Union=  0.172 [   3.127] Connected=  0.073 [   2.808]
N=    2,097,152 Union=  0.434 [   2.523] Connected=  0.255 [   3.493]
N=    4,194,304 Union=  0.991 [   2.283] Connected=  0.482 [   1.890]
N=    8,388,608 Union=  1.682 [   1.697] Connected=  0.937 [   1.944]
N=   16,777,216 Union=  4.240 [   2.521] Connected=  2.861 [   3.053]
N=   33,554,432 Union=  8.646 [   2.039] Connected=  5.419 [   1.894]

Even faster

Weighted Compression Halving [9/10]

  public int find(int p) {
    int root = p;
    while (root != id[root]) {
      id[root] = id[id[root]];
      root = id[root];
    }



    return root;
  }

  public void union(int p, int q) {
    int pid = find(p); // loser
    int qid = find(q); // champion
    if (pid == qid) return;
    if (sz[qid] > sz[pid]) { id[pid] = qid; sz[qid] += sz[pid]; }
    else                   { id[qid] = pid; sz[pid] += sz[qid]; }
    count--;
  }

Output

       10[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
 4  3:  9[0, 1, 2, 4, 4, 5, 6, 7, 8, 9]
 3  8:  8[0, 1, 2, 4, 4, 5, 6, 7, 4, 9]
 6  5:  7[0, 1, 2, 4, 4, 6, 6, 7, 4, 9]
 9  4:  6[0, 1, 2, 4, 4, 6, 6, 7, 4, 4]
 2  1:  5[0, 2, 2, 4, 4, 6, 6, 7, 4, 4]
 8  9: connected
 5  0:  4[6, 2, 2, 4, 4, 6, 6, 7, 4, 4]
 7  2:  3[6, 2, 2, 4, 4, 6, 6, 2, 4, 4]
 6  1:  2[6, 2, 6, 4, 4, 6, 6, 2, 4, 4]
 1  6>  2[6, 6, 6, 4, 4, 6, 6, 2, 4, 4]
 1  0: connected
 7  6>  2[6, 6, 6, 4, 4, 6, 6, 6, 4, 4]
 6  7: connected

N=          128 Union=  0.001 [Infinity] Connected=  0.000 [     NaN]
N=          256 Union=  0.000 [   0.000] Connected=  0.000 [     NaN]
N=          512 Union=  0.000 [     NaN] Connected=  0.000 [     NaN]
N=        1,024 Union=  0.000 [     NaN] Connected=  0.000 [     NaN]
N=        2,048 Union=  0.000 [     NaN] Connected=  0.001 [Infinity]
N=        4,096 Union=  0.001 [Infinity] Connected=  0.001 [   1.000]
N=        8,192 Union=  0.001 [   1.000] Connected=  0.001 [   1.000]
N=       16,384 Union=  0.003 [   3.000] Connected=  0.002 [   2.000]
N=       32,768 Union=  0.004 [   1.333] Connected=  0.001 [   0.500]
N=       65,536 Union=  0.004 [   1.000] Connected=  0.004 [   4.000]
N=      131,072 Union=  0.011 [   2.750] Connected=  0.006 [   1.500]
N=      262,144 Union=  0.032 [   2.909] Connected=  0.015 [   2.500]
N=      524,288 Union=  0.059 [   1.844] Connected=  0.022 [   1.467]
N=    1,048,576 Union=  0.132 [   2.237] Connected=  0.063 [   2.864]
N=    2,097,152 Union=  0.327 [   2.477] Connected=  0.191 [   3.032]
N=    4,194,304 Union=  0.727 [   2.223] Connected=  0.459 [   2.403]
N=    8,388,608 Union=  1.998 [   2.748] Connected=  1.056 [   2.301]
N=   16,777,216 Union=  4.947 [   2.476] Connected=  2.554 [   2.419]
N=   33,554,432 Union= 10.013 [   2.024] Connected=  6.093 [   2.386]

Also faster

Comparing UF implementations [10/10]

Suppose that we have three elements [0, 1, 2] and that we union 0 and 1, and then 1 and 2.

When we union 0 and 1, let's suppose that 1 is the champion, so the array is [1, 1, 2]. Pictorially, we have:

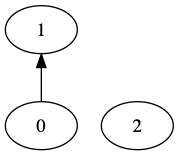
What can happen after we union 1 and 2?

For quick find, the answer 2,2,2 is possible, but this outcome is not possible for quick union, or weighted union.
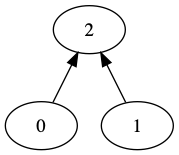
For quick union, the answer 1,2,2 is possible, but this outcome is not possible for quick find, or weighted union.
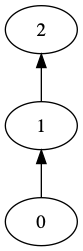
For weighted union, the only possible outcome is 1,1,1. This outcome is possible under all three algorithms.

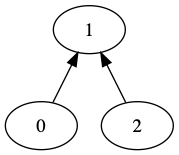
Revised: 2008/03/17 13:01