CSC300: Experiments with Time Complexity

Contents [0/19]

Video [1/19]
XCountingLoops [2/19]
2D Square [3/19]
2D Triangle [4/19]
2D Flat Pack [5/19]
2D N * lg(N) [6/19]
2D N * lg(N) - Flat Pack [7/19]
2D lg(N) * lg(N) [8/19]
3D Cube [9/19]
3D Pyramid [10/19]
4D Cube [11/19]
4D Pyramid [12/19]
5D Cube [13/19]
5D Pyramid [14/19]
XCountingRecursion [15/19]
Recursive Factorial [16/19]
Recursive Fibonacci (Terrible Version) [17/19]
String Concatenation (Recursive) [18/19]
String Concatenation (Loop) [19/19]

(Click here for one slide per page)


Video [1/19]

In three parts

Open Playlist

Open Playlist

Open Playlist

XCountingLoops [2/19]

file:XCountingLoops.java [source] [doc-public] [doc-private]
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
 
package algs14;
import stdlib.*;
public class XCountingLoops {
  // To Print: StdOut.printf ("N=%3d i=%3d N-i=%d\n", N, i, N-i);
  //
  // Test variant with one, two or three nested loops
  //
  // Outermost:
  // for (long i = 1; i <= N; i = i+1) {
  // for (long i = 1; i <= N; i = i*2) {
  //
  // Next:
  // for (long j = 1; j <= N; j = j+1) {
  // for (long j = 1; j <= i; j = j+1) {
  // for (long j = 1; j <= N; j = j*2) {
  // for (long j = 1; j <= i; j = j*2) {
  //
  // Next:
  // for (long k = 1; k <= N; k = k+1) {
  // for (long k = 1; k <= j; k = k+1) {
  // for (long k = 1; k <= N; k = k*2) {
  // for (long k = 1; k <= j; k = k*2) {

  // f counts the number of times the innermost loop executes 
  static long f (long N) {
    long result = 0;
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= N; j = j+1) {
        result = result+1;
        if (N <= 64) StdOut.format ("%02d ", i);
      }
      if (N <= 64) StdOut.println ();
    }
    return result;
  }
  public static void main (String[] args) {
    f(16);

    long MIN = 256L; // for powers of ten, start with 500L
    long MAX = 3_200_000_000L;
    Stopwatch sw = new Stopwatch ();
    double prevCount = f(MIN);
    double prevTime = sw.elapsedTime ();
    for (long N = MIN*2; N <= MAX; N=N*2) {
      sw = new Stopwatch ();
      long count = f(N);
      double time = sw.elapsedTime ();
      StdOut.format ("Elapsed count f(%,13d): %,16d: %10.3f [%10.3f : %10.3f]\n", N, count, count / prevCount, time, time/prevTime);
      //StdOut.format ("Elapsed count f(%,13d): %,16d: %10.3f\n", N, count, count / prevCount);
      prevCount = count;
      prevTime = time;
    }
  }
}

2D Square [3/19]

01
02
03
04
05
 
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= N; j = j+1) {
        result = result+1;
      }
    }

Output 

01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 
02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 
03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 03 
04 04 04 04 04 04 04 04 04 04 04 04 04 04 04 04 
05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 
06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 06 
07 07 07 07 07 07 07 07 07 07 07 07 07 07 07 07 
08 08 08 08 08 08 08 08 08 08 08 08 08 08 08 08 
09 09 09 09 09 09 09 09 09 09 09 09 09 09 09 09 
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 
11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 
12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 
13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 13 
14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 14 
15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 
16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 
Elapsed count f(          512):          262,144:      4.000 [     0.003 :      0.750]
Elapsed count f(        1,024):        1,048,576:      4.000 [     0.001 :      0.333]
Elapsed count f(        2,048):        4,194,304:      4.000 [     0.006 :      6.000]
Elapsed count f(        4,096):       16,777,216:      4.000 [     0.032 :      5.333]
Elapsed count f(        8,192):       67,108,864:      4.000 [     0.056 :      1.750]
Elapsed count f(       16,384):      268,435,456:      4.000 [     0.152 :      2.714]
Elapsed count f(       32,768):    1,073,741,824:      4.000 [     0.546 :      3.592]
Elapsed count f(       65,536):    4,294,967,296:      4.000 [     2.228 :      4.081]
Elapsed count f(      131,072):   17,179,869,184:      4.000 [     9.405 :      4.221]
Elapsed count f(      262,144):   68,719,476,736:      4.000 [    35.069 :      3.729]
Elapsed count f(      524,288) aborted execution after a minute or so
Elapsed count f(    1,048,576) aborted execution after a minute or so
Elapsed count f(    2,097,152) aborted execution after a minute or so
Elapsed count f(    4,194,304) aborted execution after a minute or so
Elapsed count f(    8,388,608) aborted execution after a minute or so
Elapsed count f(   16,777,216) aborted execution after a minute or so
Elapsed count f(   33,554,432) aborted execution after a minute or so
Elapsed count f(   67,108,864) aborted execution after a minute or so
Elapsed count f(  134,217,728) aborted execution after a minute or so
Elapsed count f(  268,435,456) aborted execution after a minute or so
Elapsed count f(  536,870,912) aborted execution after a minute or so
Elapsed count f(1,073,741,824) aborted execution after a minute or so
Elapsed count f(2,147,483,648) aborted execution after a minute or so

This is quadratic: ~ N^2

2D Triangle [4/19]

01
02
03
04
05
 
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= i; j = j+1) {
        result = result+1;
      }
    }

Output 

01 
02 02 
03 03 03 
04 04 04 04 
05 05 05 05 05 
06 06 06 06 06 06 
07 07 07 07 07 07 07 
08 08 08 08 08 08 08 08 
09 09 09 09 09 09 09 09 09 
10 10 10 10 10 10 10 10 10 10 
11 11 11 11 11 11 11 11 11 11 11 
12 12 12 12 12 12 12 12 12 12 12 12 
13 13 13 13 13 13 13 13 13 13 13 13 13 
14 14 14 14 14 14 14 14 14 14 14 14 14 14 
15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 
16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 
Elapsed count f(          512):          131,328:      3.992 [     0.002 :      2.000]
Elapsed count f(        1,024):          524,800:      3.996 [     0.003 :      1.500]
Elapsed count f(        2,048):        2,098,176:      3.998 [     0.002 :      0.667]
Elapsed count f(        4,096):        8,390,656:      3.999 [     0.005 :      2.500]
Elapsed count f(        8,192):       33,558,528:      4.000 [     0.016 :      3.200]
Elapsed count f(       16,384):      134,225,920:      4.000 [     0.065 :      4.063]
Elapsed count f(       32,768):      536,887,296:      4.000 [     0.246 :      3.785]
Elapsed count f(       65,536):    2,147,516,416:      4.000 [     1.001 :      4.069]
Elapsed count f(      131,072):    8,590,000,128:      4.000 [     4.006 :      4.002]
Elapsed count f(      262,144):   34,359,869,440:      4.000 [    15.628 :      3.901]
Elapsed count f(      524,288):  137,439,215,616:      4.000 [    62.422 :      3.994]
Elapsed count f(    1,048,576) aborted execution after a minute or so
Elapsed count f(    2,097,152) aborted execution after a minute or so
Elapsed count f(    4,194,304) aborted execution after a minute or so
Elapsed count f(    8,388,608) aborted execution after a minute or so
Elapsed count f(   16,777,216) aborted execution after a minute or so
Elapsed count f(   33,554,432) aborted execution after a minute or so
Elapsed count f(   67,108,864) aborted execution after a minute or so
Elapsed count f(  134,217,728) aborted execution after a minute or so
Elapsed count f(  268,435,456) aborted execution after a minute or so
Elapsed count f(  536,870,912) aborted execution after a minute or so
Elapsed count f(1,073,741,824) aborted execution after a minute or so
Elapsed count f(2,147,483,648) aborted execution after a minute or so

This is quadratic: ~ 1/2 * N^2

More accurately: (1/2 * N^2) - N/2

2D Flat Pack [5/19]

01
02
03
04
05
 
    for (long i = 1; i <= N; i = i*2) {
      for (long j = 1; j <= i; j = j+1) {
        result = result+1;
      }
    }

Output 

01 
02 02 
04 04 04 04 
08 08 08 08 08 08 08 08 
16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 











Elapsed count f(          512):            1,023:      2.002 [     0.000 :        NaN]
Elapsed count f(        1,024):            2,047:      2.001 [     0.000 :        NaN]
Elapsed count f(        2,048):            4,095:      2.000 [     0.001 :   Infinity]
Elapsed count f(        4,096):            8,191:      2.000 [     0.000 :      0.000]
Elapsed count f(        8,192):           16,383:      2.000 [     0.001 :   Infinity]
Elapsed count f(       16,384):           32,767:      2.000 [     0.003 :      3.000]
Elapsed count f(       32,768):           65,535:      2.000 [     0.001 :      0.333]
Elapsed count f(       65,536):          131,071:      2.000 [     0.003 :      3.000]
Elapsed count f(      131,072):          262,143:      2.000 [     0.000 :      0.000]
Elapsed count f(      262,144):          524,287:      2.000 [     0.001 :   Infinity]
Elapsed count f(      524,288):        1,048,575:      2.000 [     0.001 :      1.000]
Elapsed count f(    1,048,576):        2,097,151:      2.000 [     0.002 :      2.000]
Elapsed count f(    2,097,152):        4,194,303:      2.000 [     0.003 :      1.500]
Elapsed count f(    4,194,304):        8,388,607:      2.000 [     0.010 :      3.333]
Elapsed count f(    8,388,608):       16,777,215:      2.000 [     0.019 :      1.900]
Elapsed count f(   16,777,216):       33,554,431:      2.000 [     0.033 :      1.737]
Elapsed count f(   33,554,432):       67,108,863:      2.000 [     0.041 :      1.242]
Elapsed count f(   67,108,864):      134,217,727:      2.000 [     0.092 :      2.244]
Elapsed count f(  134,217,728):      268,435,455:      2.000 [     0.169 :      1.837]
Elapsed count f(  268,435,456):      536,870,911:      2.000 [     0.292 :      1.728]
Elapsed count f(  536,870,912):    1,073,741,823:      2.000 [     0.553 :      1.894]
Elapsed count f(1,073,741,824):    2,147,483,647:      2.000 [     1.149 :      2.078]
Elapsed count f(2,147,483,648):    4,294,967,295:      2.000 [     2.284 :      1.988]

This is linear: ~ 2N

More accurately: 2N - 1

2D N * lg(N) [6/19]

01
02
03
04
05
 
    for (long i = 1; i <= N; i = i*2) {
      for (long j = 1; j <= N; j = j+1) {
        result = result+1;
      }
    }

Output 

01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 
02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 02 
04 04 04 04 04 04 04 04 04 04 04 04 04 04 04 04 
08 08 08 08 08 08 08 08 08 08 08 08 08 08 08 08 
16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 











Elapsed count f(          512):            5,120:      2.222 [     0.000 :        NaN]
Elapsed count f(        1,024):           11,264:      2.200 [     0.001 :   Infinity]
Elapsed count f(        2,048):           24,576:      2.182 [     0.001 :      1.000]
Elapsed count f(        4,096):           53,248:      2.167 [     0.001 :      1.000]
Elapsed count f(        8,192):          114,688:      2.154 [     0.000 :      0.000]
Elapsed count f(       16,384):          245,760:      2.143 [     0.002 :   Infinity]
Elapsed count f(       32,768):          524,288:      2.133 [     0.001 :      0.500]
Elapsed count f(       65,536):        1,114,112:      2.125 [     0.001 :      1.000]
Elapsed count f(      131,072):        2,359,296:      2.118 [     0.001 :      1.000]
Elapsed count f(      262,144):        4,980,736:      2.111 [     0.003 :      3.000]
Elapsed count f(      524,288):       10,485,760:      2.105 [     0.006 :      2.000]
Elapsed count f(    1,048,576):       22,020,096:      2.100 [     0.014 :      2.333]
Elapsed count f(    2,097,152):       46,137,344:      2.095 [     0.030 :      2.143]
Elapsed count f(    4,194,304):       96,468,992:      2.091 [     0.054 :      1.800]
Elapsed count f(    8,388,608):      201,326,592:      2.087 [     0.108 :      2.000]
Elapsed count f(   16,777,216):      419,430,400:      2.083 [     0.222 :      2.056]
Elapsed count f(   33,554,432):      872,415,232:      2.080 [     0.505 :      2.275]
Elapsed count f(   67,108,864):    1,811,939,328:      2.077 [     0.972 :      1.925]
Elapsed count f(  134,217,728):    3,758,096,384:      2.074 [     2.057 :      2.116]
Elapsed count f(  268,435,456):    7,784,628,224:      2.071 [     4.106 :      1.996]
Elapsed count f(  536,870,912):   16,106,127,360:      2.069 [     8.241 :      2.007]
Elapsed count f(1,073,741,824):   33,285,996,544:      2.067 [    17.254 :      2.094]
Elapsed count f(2,147,483,648):   68,719,476,736:      2.065 [    35.660 :      2.067]

This is linearithmic: ~ N * lg(N)

2D N * lg(N) - Flat Pack [7/19]

01
02
03
04
05
 
    for (long i = 1; i <= N; i = i*2) {
      for (long j = i + 1; j <= N; j = j+1) {
        result = result+1;
      }
    }

Output 

01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 
02 02 02 02 02 02 02 02 02 02 02 02 02 02 
04 04 04 04 04 04 04 04 04 04 04 04 
08 08 08 08 08 08 08 08 












Elapsed count f(          512):            4,097:      2.285 [     0.001 :   Infinity]
Elapsed count f(        1,024):            9,217:      2.250 [     0.001 :      1.000]
Elapsed count f(        2,048):           20,481:      2.222 [     0.001 :      1.000]
Elapsed count f(        4,096):           45,057:      2.200 [     0.001 :      1.000]
Elapsed count f(        8,192):           98,305:      2.182 [     0.000 :      0.000]
Elapsed count f(       16,384):          212,993:      2.167 [     0.001 :   Infinity]
Elapsed count f(       32,768):          458,753:      2.154 [     0.001 :      1.000]
Elapsed count f(       65,536):          983,041:      2.143 [     0.000 :      0.000]
Elapsed count f(      131,072):        2,097,153:      2.133 [     0.002 :   Infinity]
Elapsed count f(      262,144):        4,456,449:      2.125 [     0.003 :      1.500]
Elapsed count f(      524,288):        9,437,185:      2.118 [     0.006 :      2.000]
Elapsed count f(    1,048,576):       19,922,945:      2.111 [     0.013 :      2.167]
Elapsed count f(    2,097,152):       41,943,041:      2.105 [     0.026 :      2.000]
Elapsed count f(    4,194,304):       88,080,385:      2.100 [     0.057 :      2.192]
Elapsed count f(    8,388,608):      184,549,377:      2.095 [     0.145 :      2.544]
Elapsed count f(   16,777,216):      385,875,969:      2.091 [     0.260 :      1.793]
Elapsed count f(   33,554,432):      805,306,369:      2.087 [     0.517 :      1.988]
Elapsed count f(   67,108,864):    1,677,721,601:      2.083 [     1.020 :      1.973]
Elapsed count f(  134,217,728):    3,489,660,929:      2.080 [     2.126 :      2.084]
Elapsed count f(  268,435,456):    7,247,757,313:      2.077 [     4.608 :      2.167]
Elapsed count f(  536,870,912):   15,032,385,537:      2.074 [     9.334 :      2.026]
Elapsed count f(1,073,741,824):   31,138,512,897:      2.071 [    19.133 :      2.050]
Elapsed count f(2,147,483,648):   64,424,509,441:      2.069 [    40.003 :      2.091]

This is linearithmic: ~ N * lg(N)

More accurately: (N * lg(N)) - (2N - 1)

2D lg(N) * lg(N) [8/19]

01
02
03
04
05
 
    for (long i = 1; i <= N; i = i*2) {
      for (long j = 1; j <= N; j = j*2) {
        result = result+1;
      }
    }

Output 

01 01 01 01 01 
02 02 02 02 02 
04 04 04 04 04 
08 08 08 08 08 
16 16 16 16 16 











Elapsed count f(          512):              100:      1.235 [     0.000 :        NaN]
Elapsed count f(        1,024):              121:      1.210 [     0.000 :        NaN]
Elapsed count f(        2,048):              144:      1.190 [     0.000 :        NaN]
Elapsed count f(        4,096):              169:      1.174 [     0.000 :        NaN]
Elapsed count f(        8,192):              196:      1.160 [     0.000 :        NaN]
Elapsed count f(       16,384):              225:      1.148 [     0.000 :        NaN]
Elapsed count f(       32,768):              256:      1.138 [     0.000 :        NaN]
Elapsed count f(       65,536):              289:      1.129 [     0.000 :        NaN]
Elapsed count f(      131,072):              324:      1.121 [     0.000 :        NaN]
Elapsed count f(      262,144):              361:      1.114 [     0.000 :        NaN]
Elapsed count f(      524,288):              400:      1.108 [     0.000 :        NaN]
Elapsed count f(    1,048,576):              441:      1.103 [     0.000 :        NaN]
Elapsed count f(    2,097,152):              484:      1.098 [     0.000 :        NaN]
Elapsed count f(    4,194,304):              529:      1.093 [     0.000 :        NaN]
Elapsed count f(    8,388,608):              576:      1.089 [     0.000 :        NaN]
Elapsed count f(   16,777,216):              625:      1.085 [     0.000 :        NaN]
Elapsed count f(   33,554,432):              676:      1.082 [     0.000 :        NaN]
Elapsed count f(   67,108,864):              729:      1.078 [     0.000 :        NaN]
Elapsed count f(  134,217,728):              784:      1.075 [     0.000 :        NaN]
Elapsed count f(  268,435,456):              841:      1.073 [     0.000 :        NaN]
Elapsed count f(  536,870,912):              900:      1.070 [     0.001 :   Infinity]
Elapsed count f(1,073,741,824):              961:      1.068 [     0.000 :      0.000]
Elapsed count f(2,147,483,648):            1,024:      1.066 [     0.000 :        NaN]

This is log squared: ~ lg(N) * lg(N)

3D Cube [9/19]

01
02
03
04
05
06
07
 
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= N; j = j+1) {
        for (long k = 1; k <= N; k = k+1) {
          result = result+1;          
        }
      }
    }

Output 









Elapsed count f(            8):              512:      8.000 [     0.000 :        NaN]
Elapsed count f(           16):            4,096:      8.000 [     0.000 :        NaN]
Elapsed count f(           32):           32,768:      8.000 [     0.000 :        NaN]
Elapsed count f(           64):          262,144:      8.000 [     0.001 :   Infinity]
Elapsed count f(          128):        2,097,152:      8.000 [     0.004 :      4.000]
Elapsed count f(          256):       16,777,216:      8.000 [     0.008 :      2.000]
Elapsed count f(          512):      134,217,728:      8.000 [     0.063 :      7.875]
Elapsed count f(        1,024):    1,073,741,824:      8.000 [     0.532 :      8.444]
Elapsed count f(        2,048):    8,589,934,592:      8.000 [     3.979 :      7.479]
Elapsed count f(        4,096):   68,719,476,736:      8.000 [    31.300 :      7.866]
Elapsed count f(        8,192):  549,755,813,888:      8.000 [   253.206 :      8.090]
Elapsed count f(       16,384) aborted execution after a minute or so
Elapsed count f(       32,768) aborted execution after a minute or so
Elapsed count f(       65,536) aborted execution after a minute or so
Elapsed count f(      131,072) aborted execution after a minute or so
Elapsed count f(      262,144) aborted execution after a minute or so
Elapsed count f(      524,288) aborted execution after a minute or so
Elapsed count f(    1,048,576) aborted execution after a minute or so
Elapsed count f(    2,097,152) aborted execution after a minute or so
Elapsed count f(    4,194,304) aborted execution after a minute or so
Elapsed count f(    8,388,608) aborted execution after a minute or so
Elapsed count f(   16,777,216) aborted execution after a minute or so
Elapsed count f(   33,554,432) aborted execution after a minute or so
Elapsed count f(   67,108,864) aborted execution after a minute or so
Elapsed count f(  134,217,728) aborted execution after a minute or so
Elapsed count f(  268,435,456) aborted execution after a minute or so
Elapsed count f(  536,870,912) aborted execution after a minute or so
Elapsed count f(1,073,741,824) aborted execution after a minute or so
Elapsed count f(2,147,483,648) aborted execution after a minute or so

This is cubic: ~ N^3

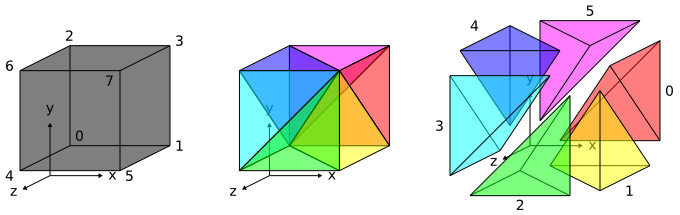
3D Pyramid [10/19]

01
02
03
04
05
06
07
 
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= i; j = j+1) {
        for (long k = 1; k <= j; k = k+1) {
          result = result+1;          
        }
      }
    }

Output 









Elapsed count f(            8):              120:      6.000 [     0.000 :        NaN]
Elapsed count f(           16):              816:      6.800 [     0.000 :        NaN]
Elapsed count f(           32):            5,984:      7.333 [     0.000 :        NaN]
Elapsed count f(           64):           45,760:      7.647 [     0.001 :   Infinity]
Elapsed count f(          128):          357,760:      7.818 [     0.001 :      1.000]
Elapsed count f(          256):        2,829,056:      7.908 [     0.005 :      5.000]
Elapsed count f(          512):       22,500,864:      7.953 [     0.011 :      2.200]
Elapsed count f(        1,024):      179,481,600:      7.977 [     0.091 :      8.273]
Elapsed count f(        2,048):    1,433,753,600:      7.988 [     0.683 :      7.505]
Elapsed count f(        4,096):   11,461,636,096:      7.994 [     5.322 :      7.792]
Elapsed count f(        8,192):   91,659,526,144:      7.997 [    42.736 :      8.030]
Elapsed count f(       16,384) aborted execution after a minute or so
Elapsed count f(       32,768) aborted execution after a minute or so
Elapsed count f(       65,536) aborted execution after a minute or so
Elapsed count f(      131,072) aborted execution after a minute or so
Elapsed count f(      262,144) aborted execution after a minute or so
Elapsed count f(      524,288) aborted execution after a minute or so
Elapsed count f(    1,048,576) aborted execution after a minute or so
Elapsed count f(    2,097,152) aborted execution after a minute or so
Elapsed count f(    4,194,304) aborted execution after a minute or so
Elapsed count f(    8,388,608) aborted execution after a minute or so
Elapsed count f(   16,777,216) aborted execution after a minute or so
Elapsed count f(   33,554,432) aborted execution after a minute or so
Elapsed count f(   67,108,864) aborted execution after a minute or so
Elapsed count f(  134,217,728) aborted execution after a minute or so
Elapsed count f(  268,435,456) aborted execution after a minute or so
Elapsed count f(  536,870,912) aborted execution after a minute or so
Elapsed count f(1,073,741,824) aborted execution after a minute or so
Elapsed count f(2,147,483,648) aborted execution after a minute or so

This is cubic: ~ 1/6 * N^3

It's a tetrahedron (image from Dune Project):

tetrahedron

4D Cube [11/19]

01
02
03
04
05
06
07
08
09
 
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= N; j = j+1) {
        for (long k = 1; k <= N; k = k+1) {
          for (long l = 1; l <= N; l = l+1) {
            result = result+1;
          }
        }
      }
    }

Output 







Elapsed count f(            8):            4,096:     16.000 [     0.000 :        NaN]
Elapsed count f(           16):           65,536:     16.000 [     0.000 :        NaN]
Elapsed count f(           32):        1,048,576:     16.000 [     0.003 :   Infinity]
Elapsed count f(           64):       16,777,216:     16.000 [     0.026 :      8.667]
Elapsed count f(          128):      268,435,456:     16.000 [     0.140 :      5.385]
Elapsed count f(          256):    4,294,967,296:     16.000 [     2.014 :     14.386]
Elapsed count f(          512):   68,719,476,736:     16.000 [    31.673 :     15.726]
Elapsed count f(        1,024) aborted execution after a minute or so
Elapsed count f(        2,048) aborted execution after a minute or so
Elapsed count f(        4,096) aborted execution after a minute or so
Elapsed count f(        8,192) aborted execution after a minute or so
Elapsed count f(       16,384) aborted execution after a minute or so
Elapsed count f(       32,768) aborted execution after a minute or so
Elapsed count f(       65,536) aborted execution after a minute or so
Elapsed count f(      131,072) aborted execution after a minute or so
Elapsed count f(      262,144) aborted execution after a minute or so
Elapsed count f(      524,288) aborted execution after a minute or so
Elapsed count f(    1,048,576) aborted execution after a minute or so
Elapsed count f(    2,097,152) aborted execution after a minute or so
Elapsed count f(    4,194,304) aborted execution after a minute or so
Elapsed count f(    8,388,608) aborted execution after a minute or so
Elapsed count f(   16,777,216) aborted execution after a minute or so
Elapsed count f(   33,554,432) aborted execution after a minute or so
Elapsed count f(   67,108,864) aborted execution after a minute or so
Elapsed count f(  134,217,728) aborted execution after a minute or so
Elapsed count f(  268,435,456) aborted execution after a minute or so
Elapsed count f(  536,870,912) aborted execution after a minute or so
Elapsed count f(1,073,741,824) aborted execution after a minute or so
Elapsed count f(2,147,483,648) aborted execution after a minute or so

This is quartic: ~ N^4

4D Pyramid [12/19]

01
02
03
04
05
06
07
08
09
 
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= i; j = j+1) {
        for (long k = 1; k <= j; k = k+1) {
          for (long l = 1; l <= k; l = l+1) {
            result = result+1;
          }
        }
      }
    }

Output 







Elapsed count f(            8):              330:      9.429 [     0.000 :        NaN]
Elapsed count f(           16):            3,876:     11.745 [     0.001 :   Infinity]
Elapsed count f(           32):           52,360:     13.509 [     0.001 :      1.000]
Elapsed count f(           64):          766,480:     14.639 [     0.002 :      2.000]
Elapsed count f(          128):       11,716,640:     15.286 [     0.008 :      4.000]
Elapsed count f(          256):      183,181,376:     15.634 [     0.277 :     34.625]
Elapsed count f(          512):    2,896,986,240:     15.815 [     4.417 :     15.946]
Elapsed count f(        1,024):   46,081,900,800:     15.907 [    68.227 :     15.446]
Elapsed count f(        2,048) aborted execution after a minute or so
Elapsed count f(        4,096) aborted execution after a minute or so
Elapsed count f(        8,192) aborted execution after a minute or so
Elapsed count f(       16,384) aborted execution after a minute or so
Elapsed count f(       32,768) aborted execution after a minute or so
Elapsed count f(       65,536) aborted execution after a minute or so
Elapsed count f(      131,072) aborted execution after a minute or so
Elapsed count f(      262,144) aborted execution after a minute or so
Elapsed count f(      524,288) aborted execution after a minute or so
Elapsed count f(    1,048,576) aborted execution after a minute or so
Elapsed count f(    2,097,152) aborted execution after a minute or so
Elapsed count f(    4,194,304) aborted execution after a minute or so
Elapsed count f(    8,388,608) aborted execution after a minute or so
Elapsed count f(   16,777,216) aborted execution after a minute or so
Elapsed count f(   33,554,432) aborted execution after a minute or so
Elapsed count f(   67,108,864) aborted execution after a minute or so
Elapsed count f(  134,217,728) aborted execution after a minute or so
Elapsed count f(  268,435,456) aborted execution after a minute or so
Elapsed count f(  536,870,912) aborted execution after a minute or so
Elapsed count f(1,073,741,824) aborted execution after a minute or so
Elapsed count f(2,147,483,648) aborted execution after a minute or so

This is quartic: ~ 1/24 * N^4

5D Cube [13/19]

01
02
03
04
05
06
07
08
09
10
11
 
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= N; j = j+1) {
        for (long k = 1; k <= N; k = k+1) {
          for (long l = 1; l <= N; l = l+1) {
            for (long m = 1; m <= N; m = m+1) {
              result = result+1;
            }
          }
        }
      }
    }

Output 





Elapsed count f(            8):           32,768:     32.000 [     0.000 :        NaN]
Elapsed count f(           16):        1,048,576:     32.000 [     0.000 :        NaN]
Elapsed count f(           32):       33,554,432:     32.000 [     0.014 :   Infinity]
Elapsed count f(           64):    1,073,741,824:     32.000 [     0.620 :     44.286]
Elapsed count f(          128):   34,359,738,368:     32.000 [    17.720 :     28.581]
Elapsed count f(          256) aborted execution after a minute or so
Elapsed count f(          512) aborted execution after a minute or so
Elapsed count f(        1,024) aborted execution after a minute or so
Elapsed count f(        2,048) aborted execution after a minute or so
Elapsed count f(        4,096) aborted execution after a minute or so
Elapsed count f(        8,192) aborted execution after a minute or so
Elapsed count f(       16,384) aborted execution after a minute or so
Elapsed count f(       32,768) aborted execution after a minute or so
Elapsed count f(       65,536) aborted execution after a minute or so
Elapsed count f(      131,072) aborted execution after a minute or so
Elapsed count f(      262,144) aborted execution after a minute or so
Elapsed count f(      524,288) aborted execution after a minute or so
Elapsed count f(    1,048,576) aborted execution after a minute or so
Elapsed count f(    2,097,152) aborted execution after a minute or so
Elapsed count f(    4,194,304) aborted execution after a minute or so
Elapsed count f(    8,388,608) aborted execution after a minute or so
Elapsed count f(   16,777,216) aborted execution after a minute or so
Elapsed count f(   33,554,432) aborted execution after a minute or so
Elapsed count f(   67,108,864) aborted execution after a minute or so
Elapsed count f(  134,217,728) aborted execution after a minute or so
Elapsed count f(  268,435,456) aborted execution after a minute or so
Elapsed count f(  536,870,912) aborted execution after a minute or so
Elapsed count f(1,073,741,824) aborted execution after a minute or so
Elapsed count f(2,147,483,648) aborted execution after a minute or so

This is quintic: ~ N^5

5D Pyramid [14/19]

01
02
03
04
05
06
07
08
09
10
11
 
    for (long i = 1; i <= N; i = i+1) {
      for (long j = 1; j <= i; j = j+1) {
        for (long k = 1; k <= j; k = k+1) {
          for (long l = 1; l <= k; l = l+1) {
            for (long m = 1; m <= l; m = m+1) {
              result = result+1;
            }
          }
        }
      }
    }

Output 





Elapsed count f(            8):              792:     14.143 [     0.000 :        NaN]
Elapsed count f(           16):           15,504:     19.576 [     0.001 :   Infinity]
Elapsed count f(           32):          376,992:     24.316 [     0.003 :      3.000]
Elapsed count f(           64):       10,424,128:     27.651 [     0.018 :      6.000]
Elapsed count f(          128):      309,319,296:     29.673 [     0.491 :     27.278]
Elapsed count f(          256):    9,525,431,552:     30.795 [     5.574 :     11.352]
Elapsed count f(          512) aborted execution after a minute or so
Elapsed count f(        1,024) aborted execution after a minute or so
Elapsed count f(        2,048) aborted execution after a minute or so
Elapsed count f(        4,096) aborted execution after a minute or so
Elapsed count f(        8,192) aborted execution after a minute or so
Elapsed count f(       16,384) aborted execution after a minute or so
Elapsed count f(       32,768) aborted execution after a minute or so
Elapsed count f(       65,536) aborted execution after a minute or so
Elapsed count f(      131,072) aborted execution after a minute or so
Elapsed count f(      262,144) aborted execution after a minute or so
Elapsed count f(      524,288) aborted execution after a minute or so
Elapsed count f(    1,048,576) aborted execution after a minute or so
Elapsed count f(    2,097,152) aborted execution after a minute or so
Elapsed count f(    4,194,304) aborted execution after a minute or so
Elapsed count f(    8,388,608) aborted execution after a minute or so
Elapsed count f(   16,777,216) aborted execution after a minute or so
Elapsed count f(   33,554,432) aborted execution after a minute or so
Elapsed count f(   67,108,864) aborted execution after a minute or so
Elapsed count f(  134,217,728) aborted execution after a minute or so
Elapsed count f(  268,435,456) aborted execution after a minute or so
Elapsed count f(  536,870,912) aborted execution after a minute or so
Elapsed count f(1,073,741,824) aborted execution after a minute or so
Elapsed count f(2,147,483,648) aborted execution after a minute or so

This is quintic: ~ 1/120 * N^5

XCountingRecursion [15/19]

file:XCountingRecursion.java [source] [doc-public] [doc-private]
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
 
package algs14;
import stdlib.*;
public class XCountingRecursion {
  /* testing an integer function */
  public static long f (long N) {
    if (N <= 1) {
      return 1;
    } else {
      long result = f(N-1) * N;     
      numOps = numOps + 1;
      return result;
    }
  }
//  public static String f (long N) {
//    if (N == 0) {
//      return "";
//    } else {
//      String result = "*" + f(N - 1);
//      numOps = numOps + result.length();
//      return result;
//    }
//  }
  private static long numOps;
  public static void main (String[] args) {
    long MIN = 4L; 
    long MAX = 5000L; // If too big, you may get a StackOverflowException
    Stopwatch sw = new Stopwatch ();
    numOps = 0;
    f(MIN);
    double prevCount = numOps;
    double prevTime = sw.elapsedTime ();
    for (long N = MIN*2; N <= MAX; N=N*2) {
      sw = new Stopwatch ();
      numOps = 0;
      f(N);
      long count = numOps; 
      double time = sw.elapsedTime ();
      StdOut.format ("Elapsed count f(%,13d): %,17d: %10.3f [%10.3f : %10.3f]\n", N, count, count / prevCount, time, time/prevTime);
      //StdOut.format ("Elapsed count f(%,13d): %,17d: %10.3f\n", N, count, count / prevCount);
      prevCount = count;
      prevTime = time;
    }
  }
}

Recursive Factorial [16/19]

01
02
03
04
05
06
07
08
09
 
  public static long f (long N) {
    if (N <= 1) {
      return 1;
    } else {
      long result = f(N-1) * N;     
      numOps = numOps + 1;
      return result;
    }
  }

Output 

Elapsed count f(            8):               7:      2.333 [     0.000 :        NaN]
Elapsed count f(           16):              15:      2.143 [     0.000 :        NaN]
Elapsed count f(           32):              31:      2.067 [     0.000 :        NaN]
Elapsed count f(           64):              63:      2.032 [     0.000 :        NaN]
Elapsed count f(          128):             127:      2.016 [     0.000 :        NaN]
Elapsed count f(          256):             255:      2.008 [     0.000 :        NaN]
Elapsed count f(          512):             511:      2.004 [     0.000 :        NaN]
Elapsed count f(        1,024):           1,023:      2.002 [     0.000 :        NaN]
Elapsed count f(        2,048):           2,047:      2.001 [     0.000 :        NaN]
Elapsed count f(        4,096):           4,095:      2.000 [     0.000 :        NaN]
Elapsed count f(        8,192):           8,191:      2.000 [     0.000 :        NaN]

This is linear: ~ N

Recursive Fibonacci (Terrible Version) [17/19]

01
02
03
04
05
06
07
08
09
 
  public static long f (long N) {
    if (N <= 1) {
      return N;
    } else {
      long result = f(N-1) + f(N-2);      
      numOps = numOps + 1;
      return result;
    }
  }

Output 

Elapsed count f(            8):               33:      8.250 [     0.000 :        NaN]
Elapsed count f(           16):            1,596:     48.364 [     0.000 :        NaN]
Elapsed count f(           32):        3,524,577:   2208.382 [     0.011 :   Infinity]
Elapsed count f(           64) aborted execution after a thousand hours or so
Elapsed count f(          128) aborted execution after a thousand hours or so
Elapsed count f(          256) aborted execution after a thousand hours or so
Elapsed count f(          512) aborted execution after a thousand hours or so
Elapsed count f(        1,024) aborted execution after a thousand hours or so
Elapsed count f(        2,048) aborted execution after a thousand hours or so
Elapsed count f(        4,096) aborted execution after a thousand hours or so
Elapsed count f(        8,192) aborted execution after a thousand hours or so

This is exponential: approximately 2^N

More accurately: (1.6)^N, where 1.6 = (1+sqrt(5))/2

String Concatenation (Recursive) [18/19]

01
02
03
04
05
06
07
08
09
 
  public static String f (long N) {
    if (N == 0) {
      return "";
    } else {
      String result = "*" + f(N - 1);
      numOps = numOps + result.length();
      return result;
    }
  }

Output 

Elapsed count f(            8):               36:      3.600 [     0.000 :        NaN]
Elapsed count f(           16):              136:      3.778 [     0.000 :        NaN]
Elapsed count f(           32):              528:      3.882 [     0.000 :        NaN]
Elapsed count f(           64):            2,080:      3.939 [     0.001 :   Infinity]
Elapsed count f(          128):            8,256:      3.969 [     0.000 :      0.000]
Elapsed count f(          256):           32,896:      3.984 [     0.000 :        NaN]
Elapsed count f(          512):          131,328:      3.992 [     0.000 :        NaN]
Elapsed count f(        1,024):          524,800:      3.996 [     0.001 :   Infinity]
Elapsed count f(        2,048):        2,098,176:      3.998 [     0.003 :      3.000]
Elapsed count f(        4,096):        8,390,656:      3.999 [     0.012 :      4.000]

 Exception in thread "main" java.lang.StackOverflowError
  at java.base/java.lang.StringBuilder.<init>(StringBuilder.java:124)
  at algs14.XCountingRecursion.f(XCountingRecursion.java:18)

String Concatenation (Loop) [19/19]

01
02
03
04
05
06
07
08
09
 
  public static String f (long N) {
    String result = "";
    while (N != 0) {
      N = N - 1;
      result = "*" + result;
      numOps = numOps + result.length();
    }
    return result;
  }

Output 

Elapsed count f(            8):               36:      3.600 [     0.000 :        NaN]
Elapsed count f(           16):              136:      3.778 [     0.000 :        NaN]
Elapsed count f(           32):              528:      3.882 [     0.000 :        NaN]
Elapsed count f(           64):            2,080:      3.939 [     0.000 :        NaN]
Elapsed count f(          128):            8,256:      3.969 [     0.000 :        NaN]
Elapsed count f(          256):           32,896:      3.984 [     0.000 :        NaN]
Elapsed count f(          512):          131,328:      3.992 [     0.000 :        NaN]
Elapsed count f(        1,024):          524,800:      3.996 [     0.001 :   Infinity]
Elapsed count f(        2,048):        2,098,176:      3.998 [     0.003 :      3.000]
Elapsed count f(        4,096):        8,390,656:      3.999 [     0.010 :      3.333]
Elapsed count f(        8,192):       33,558,528:      4.000 [     0.041 :      4.100]
Elapsed count f(       16,384):      134,225,920:      4.000 [     0.077 :      1.878]
Elapsed count f(       32,768):      536,887,296:      4.000 [     0.181 :      2.351]
Elapsed count f(       65,536):    2,147,516,416:      4.000 [     0.517 :      2.856]
Elapsed count f(      131,072):    8,590,000,128:      4.000 [     0.847 :      1.638]
Elapsed count f(      262,144):   34,359,869,440:      4.000 [     3.567 :      4.211]
Elapsed count f(      524,288):  137,439,215,616:      4.000 [    13.881 :      3.892]
Elapsed count f(    1,048,576):  549,756,338,176:      4.000 [    62.358 :      4.492]

This is quadratic: approximately N^2

Revised: 2008/03/17 13:01