CSC301: Week 7: Undirected Graphs (4.1)

Contents [0/9]

Homework [1/9]
Tree print prefix [2/9]
Prefix-order is depth-first [3/9]
Prefix order with loop [4/9]
Level-order is breadth-first [5/9]
General trees [6/9]
Natural style is cautious [7/9]
Over graphs [8/9]
Iterative DFS contrasted with BFS [9/9]

(Click here for one slide per page)


Homework [1/9]

Read through section 4.2 of the text.

For homework, complete the following, using only Graph and GraphGenerator from algs41. You may copy code from other classes in algs41, but you should not use the classes themselves.

In particular, you may not use BreadthFirstPaths although you may copy code from there.

The eccentricity of a vertex v is the length of the shortest path from that vertex to the furthest vertex from v. The diameter of a graph is the maximum eccentricity of any vertex. The radius of a graph is the smallest eccentricity of any vertex. A center is a vertex whose eccentricity is the radius. Implement the following API. (See the starter code on D2L.) 

public class MyGraphProperties {
  // constructor (exception if G not connected)
  MyGraphProperties(Graph G) {
  }

  // eccentricity of v
  int eccentricity(int v) {  }

  // diameter of G
  int diameter() {  }

  //  radius of G
  int radius() {  }

  // a center of G --- any one will do
  int center() {  }
}

Tree print prefix [2/9] 

    // recursive version

    public void printPre () {
        printPre (root);
        StdOut.println ();
    }
    private static void printPre (Node x) {
        if (x == null) return;

        StdOut.print (x.key + " ");
        printPre (x.left);
        printPre (x.right);
    }
 
    // iterative version

    public void printPre () {
        Stack<Node> s = new Stack<> ();
        s.push (root);
        while (!s.isEmpty ()) {
            Node x = s.pop ();
            if (x == null) continue;

            StdOut.print (x.key + " ");
            s.push (x.right);
            s.push (x.left);
        }
        StdOut.println ();
    }

Prefix-order is depth-first [3/9] 

    // prefix traversal of tree

    public void printPre () {
        printPre (root);
        StdOut.println ();
    }
    private static void printPre (Node x) {
        if (x == null) return;

        StdOut.print (x.key + " ");
        printPre (x.left);
        printPre (x.right);
    }
 
    // depth first traversal of graph
    // mark when visiting
    public void printPre () {
        printPre (root, new HashSet<Node>());
        StdOut.println ();
    }
    private static void printPre (Node x, HashSet<Node> marked) {
        if (x == null || marked.contains (x)) return;
        marked.add (x);
        StdOut.print (x.key + " ");
        printPre (x.left, marked);
        printPre (x.right, marked);
    }

Prefix order with loop [4/9] 

    // prefix order traversal of a tree

    public void printPrefix () {
        Stack<Node> s = new Stack<> ();

        s.push (root);
        while (!s.isEmpty ()) {
            Node x = s.pop ();
            if (x == null) continue;
            StdOut.print (x.key + " ");
            s.push (x.right);
            s.push (x.left); 
        }
        StdOut.println ();
    }
 
    // depth first traversal of a graph
    // mark when enqueuing
    public void printPrefix () {
        Stack<Node> s = new Stack<> ();
        HashSet<Node> marked = new HashSet<> ();
        s.push (root); marked.add (root);
        while (!s.isEmpty ()) {
            Node x = s.pop ();
            if (x == null || marked.contains (x)) continue;
            StdOut.print (x.key + " ");
            s.push (x.right); marked.add (x.right)
            s.push (x.left);  marked.add (x.left)
        }
        StdOut.println ();
    }

Level-order is breadth-first [5/9] 

    // level order traversal of a tree

    public void printLevel () {
        Queue<Node> q = new Queue<> ();

        q.enqueue (root);
        while (!q.isEmpty ()) {
            Node x = q.dequeue ();
            if (x == null) continue;
            StdOut.print (x.key + " ");
            q.enqueue (x.left);
            q.enqueue (x.right);
        }
        StdOut.println ();
    }
 
    // breadth first traversal of a graph
    // mark when enqueuing
    public void printLevel () {
        Queue<Node> q = new Queue<> ();
        HashSet<Node> marked = new HashSet<> ();
        q.enqueue (root); marked.add (root);
        while (!q.isEmpty ()) {
            Node x = q.dequeue ();
            if (x == null || marked.contains (x)) continue;
            StdOut.print (x.key + " ");
            q.enqueue (x.left);  marked.add (x.left)
            q.enqueue (x.right); marked.add (x.right)
        }
        StdOut.println ();
    }

General trees [6/9]

To get closer to the code for graphs, consider general trees, such as the following.

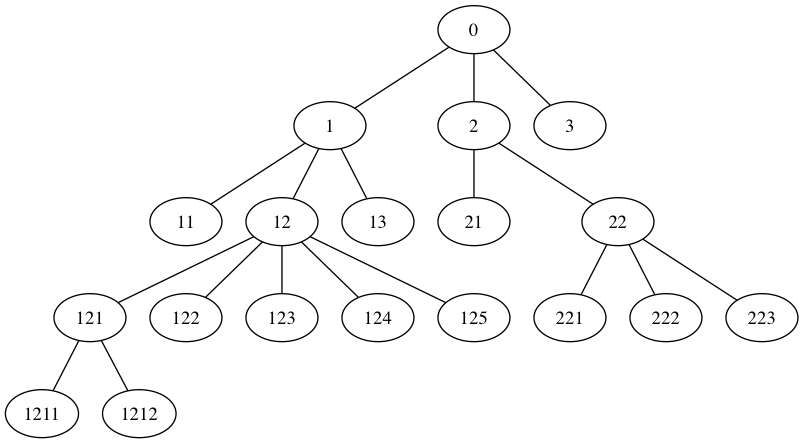
xtree

file:XTree.java [source] [doc-public] [doc-private]
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
 
package algs32;
import java.util.Scanner;
import algs13.Queue;
import stdlib.*;

public class XTree {
  private Node root;
  private XTree (Node root) { this.root = root; }
  private static class Node {
    public final int val;
    public final Queue<Node> children; // children must not be null
    public Node (int val) {
      this.val = val;
      this.children = new Queue<>();
    }
  }

  // tree input has the form "num ( ... )"
  // where num is an integer and ... is another tree input
  // example: "0 ( 1 ( 11 12 13 ) 2 ( 21 22 ( 221 222 223 ) ) 3 ( ) 4 )"
  // empty parens "( )" are optional.
  public static XTree parse (String in) {
    Scanner sc = new Scanner (in);
    Node root = parseHelper (sc);
    return new XTree (root);
  }
  private static Node parseHelper (Scanner sc) {
    int val = sc.nextInt ();
    Node result = new Node (val);
    if (sc.hasNext ("\\(")) {
      sc.next (); // gobble "("
      while (sc.hasNextInt ()) {
        Node child = parseHelper (sc);
        result.children.enqueue (child);
      }
      sc.next ("\\)"); //gobble ")"
    }
    return result;
  }

  // prefix with parenthesis
  public String toString() {
    StringBuilder sb = new StringBuilder();
    if (root != null) toString (sb, root);
    return sb.toString ();
  }
  private static void toString (StringBuilder sb, Node n) {
    sb.append (n.val);
    sb.append (" ");
    if (!n.children.isEmpty ()) {
      sb.append ("( ");
      for (Node child : n.children)
        toString (sb, child);
      sb.append (") ");
    }
  }

  public void toGraphviz(String filename) {
    GraphvizBuilder gb = new GraphvizBuilder ();
    if (root != null) toGraphviz (gb, null, root);
    gb.toFileUndirected (filename, "ordering=\"out\"");
  }
  private static void toGraphviz (GraphvizBuilder gb, Node parent, Node n) {
    gb.addLabeledNode (n, Integer.toString (n.val));
    if (parent != null) gb.addEdge (parent, n);
    for (Node child : n.children)
      toGraphviz (gb, n, child);
  }

  // prefix order traversal
  public void printPre () {
    if (root != null) printPre (root);
    StdOut.println ();
  }
  private static void printPre (Node n) {
    StdOut.print (n.val + " ");
    for (Node child : n.children) {
      printPre (child);
    }
  }

  // level order traversal
  public void printLevel () {
    Queue<Node> queue = new Queue<>();
    if (root != null) queue.enqueue(root);
    while (!queue.isEmpty()) {
      Node n = queue.dequeue();
      StdOut.print (n.val + " ");
      for (Node child : n.children) {
        queue.enqueue(child);
      }
    }
    StdOut.println ();
  }

  public static void main(String[] args) {
    XTree xtree = XTree.parse ("0 ( 1 ( 11 12 ( 121 ( 1211 1212 ) 122 123 124 125 ) 13 ) 2 ( 21 22 ( 221 222 223 ) ) 3 )");
    StdOut.println (xtree);
    xtree.printPre ();
    xtree.printLevel ();
    xtree.toGraphviz ("xtree.png");
  }
}

Natural style is cautious [7/9] 

    // prefix order traversal
    public void printPre () {
        if (root != null) printPre (root);
        StdOut.println ();
    }
    private static void printPre (Node n) {
        StdOut.print (n.val + " ");
        for (Node child : n.children) {
            printPre (child);
        }
    }
 
    // level order traversal
    public void printLevel () {
        Queue<Node> queue = new Queue<>();
        if (root != null) queue.enqueue(root);
        while (!queue.isEmpty()) {
            Node n = queue.dequeue();
            StdOut.print (n.val + " ");
            for (Node child : n.children) {
                queue.enqueue(child);
            }
        }
        StdOut.println ();
    }

Since there are a variable number of children, it makes sense to disallow null children.

Only the root can be null.

Cautious stye is natural here, since we do not need to check nullity except at the root.

Over graphs [8/9] 

    // TREE code

    // prefix order traversal
    public void printPre () {
        if (root != null) printPre (root);
        StdOut.println ();
    }
    private static void printPre (Node n) {
        StdOut.print (n.val + " ");

        for (Node child : n.children) {

            printPre (child, marked);
        }
    }

     // level order traversal
     public void printLevel () {
         Queue<Node> queue = new Queue<>();

         if (root != null) queue.enqueue(root);
         while (!queue.isEmpty()) {
             Node n = queue.dequeue();
             StdOut.print (n.val + " ");
             for (Node child : n.children) {

                 queue.enqueue(child);
             }
         }
         StdOut.println ();
     }
    }
 
    // GRAPH code

    // preorder traversal
    public void printPre () {
        if (root != null) printPre (root, new HashSet<Node> ());
        StdOut.println ();
    }
    private static void printPre (Node n, HashSet<Node> marked) {
        StdOut.print (n.val + " ");
        marked.add (n);
        for (Node child : n.children) {
            if (!marked.contains (child))
                printPre (child, marked);
        }
    }

    // level order traversal
    public void printLevel () {
        Queue<Node> queue = new Queue<> ();
        HashSet<Node> marked = new HashSet<> ();
        if (root != null) { queue.enqueue(root); marked.add (root); }
        while (!queue.isEmpty()) {
            Node n = queue.dequeue();
            StdOut.print (n.val + " ");
            for (Node child : n.children) {
                if (!marked.contains (child))
                    { queue.enqueue(child); marked.add (n); }
            }
        }
        StdOut.println ();
    }

Iterative DFS contrasted with BFS [9/9] 

// DFS -- mark when pushing
public void printPre () {
    Stack<Node> stack = new Stack<> ();
    HashSet<Node> marked = new HashSet<> ();
    if (root != null) { stack.push (root); marked.add (root); }
    while (!stack.isEmpty()) {
        Node n = stack.pop ();
        StdOut.print (n.val + " ");
        for (Node child : n.children) {
            if (!marked.contains (child))
                { stack.push (child); marked.add (n); }
        }
    }
    StdOut.println ();
}
 
  // BFS -- mark when enqueuing
  public void printLevel () {
      Queue<Node> queue = new Queue<> ();
      HashSet<Node> marked = new HashSet<> ();
      if (root != null) { queue.enqueue (root); marked.add (root); }
      while (!queue.isEmpty()) {
          Node n = queue.dequeue();
          StdOut.print (n.val + " ");
          for (Node child : n.children) {
              if (!marked.contains (child))
                  { queue.enqueue (child); marked.add (n); }
          }
      }
      StdOut.println ();
  }

Revised: 2008/03/17 13:01